10. 双晶体管电路·多级放大电路

双晶体管电路

所有模拟电路都是通过使用数量非常有限的基本结构模块来构建的，因此，对这些简单模块的透彻了解对于深入了解更复杂的电路原理至关重要，这就是为什么将它们分别考虑并进行详细分析的原因。我们已经对单晶体管电路有了全面的了解，接下来我们将专注于电流镜和差分对的探讨，这些构成了所有模拟设计的基石。
基本的双晶体管配置有：电流镜(Current Mirror)和差分对(Difference Pair)两种。

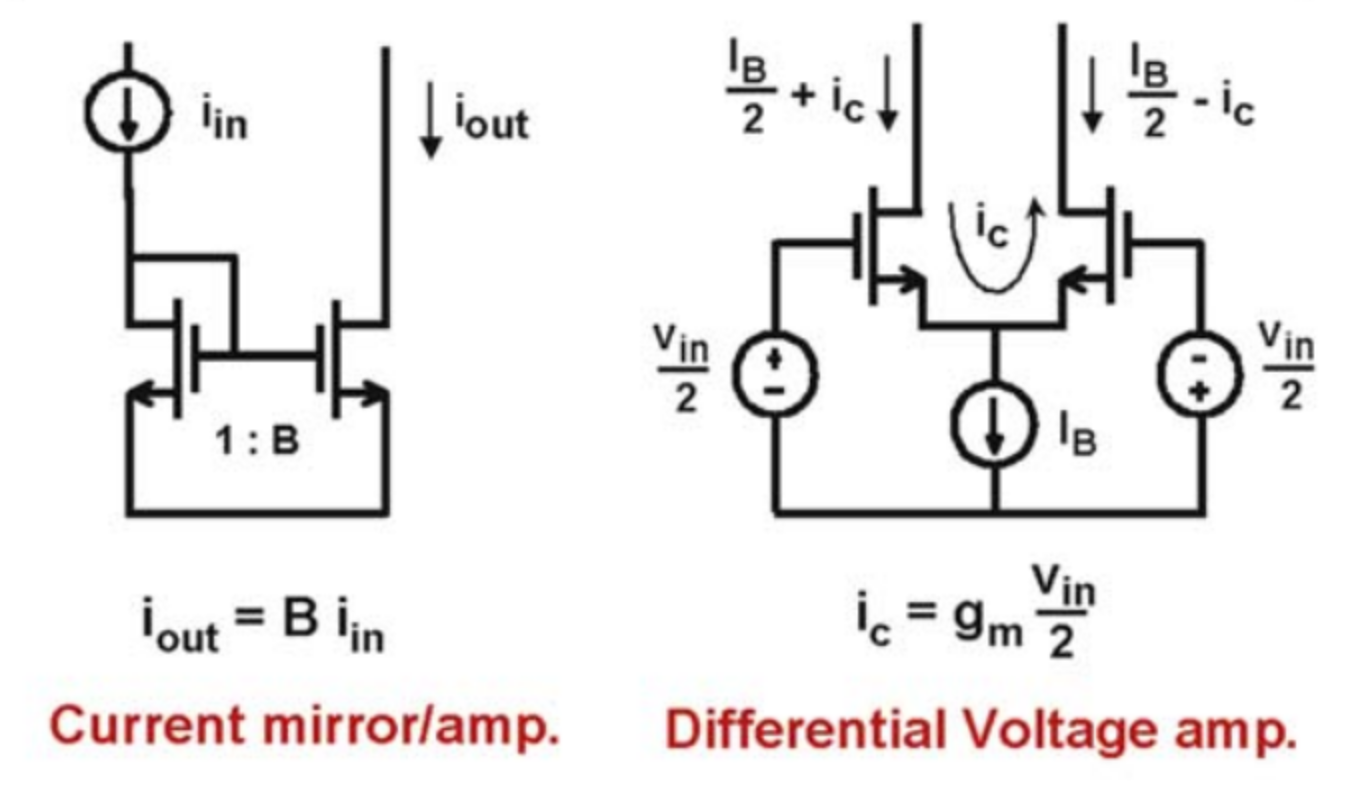
大部分模拟电路在集成电路设计中都可以通过数个多级的如上所示的两个基本电路而构成。

参考资料:https://www.icfedu.cn/archives/13594 【网站已失效】

电流镜

电流镜电路的基本设计如图所示：

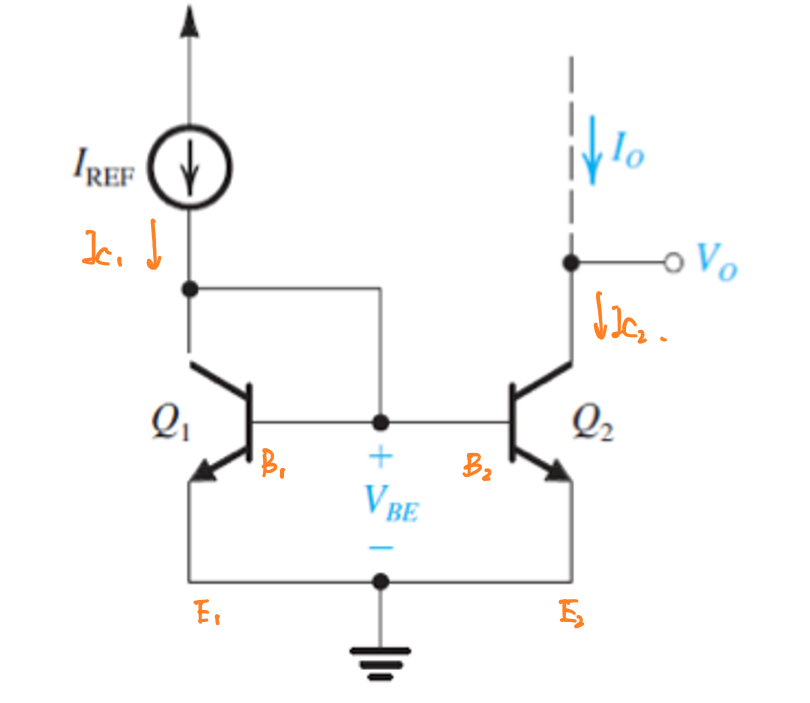
这个电路中，左边的晶体管\(Q_1\)将输入电流转为电压\(V_{BE}\)输出，右边的晶体管\(Q_2\)将\(V_{BE}\)视为输入，进而转为电流\(I_O\)输出。

电流分析

对电流镜电路，假设图中AB两点间的电流为\(2\frac{I_C}{β}\)：

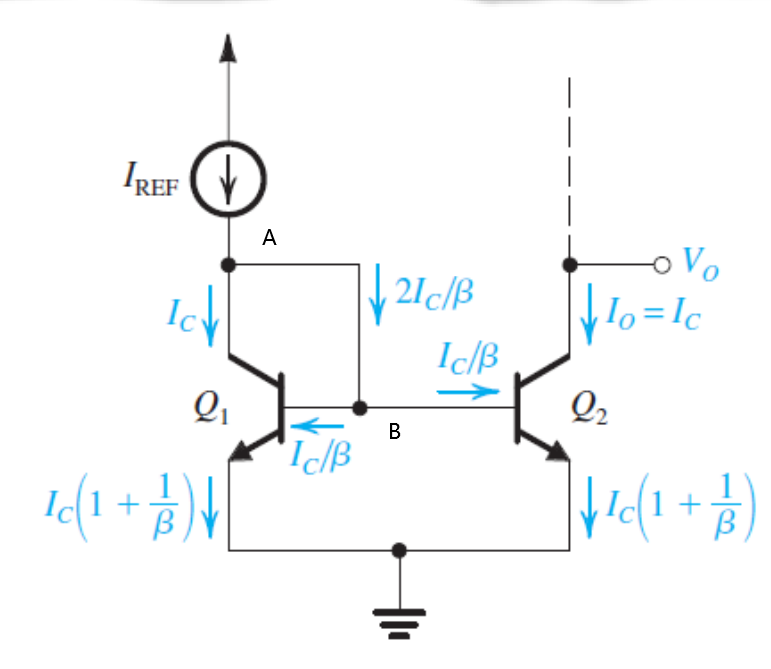
那么可以发现：
\[I_{REF}=I_C+2\frac{I_C}{β}\] \[I_O=I_C\] 因此:
\[\frac{I_O}{I_{REF}}=\frac{1}{1+\frac{2}{β}}\] 当\(β→∞\)时，\(\frac{I_O}{I_{REF}}→1\)。
通常认为\(I_O=I_{REF}\)。

带基极电流补偿的电流镜

在电流镜电路中的AB两点增加一个晶体管：

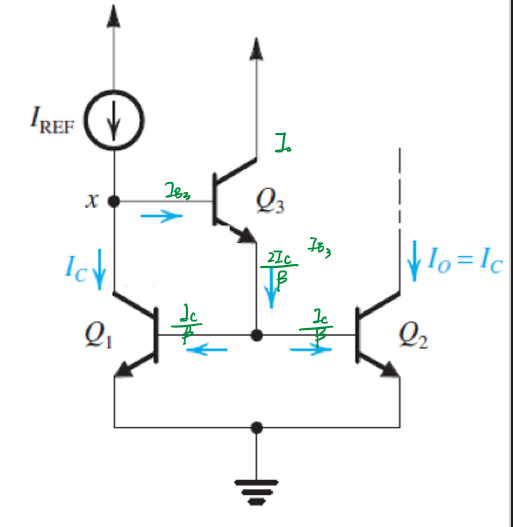
由于晶体管的存在，此时：
\[I_{REF}=I_C+I_{B3}\] \[I_{B3}=\frac{I_{E3}}{β+1}=\frac{2I_C}{β(β+1)}\] 因此：
\[I_O=I_{C}=\frac{I_{REF}}{1+\frac{2}{β(β+1)}}\] 相比于原来的电流镜电路，输出的电流大小对β的依赖性更低，更加稳定。

基本增益单元

\(I_{REF}\)的产生方式有两种：第一种是通过给电压，使用电阻将电压转换为电流。另一种是直接给一个电流源。
在集成电路设计中第一种方法无法精准控制电流的大小，因此通常采用第二种方法来获得\(I_{REF}\)。

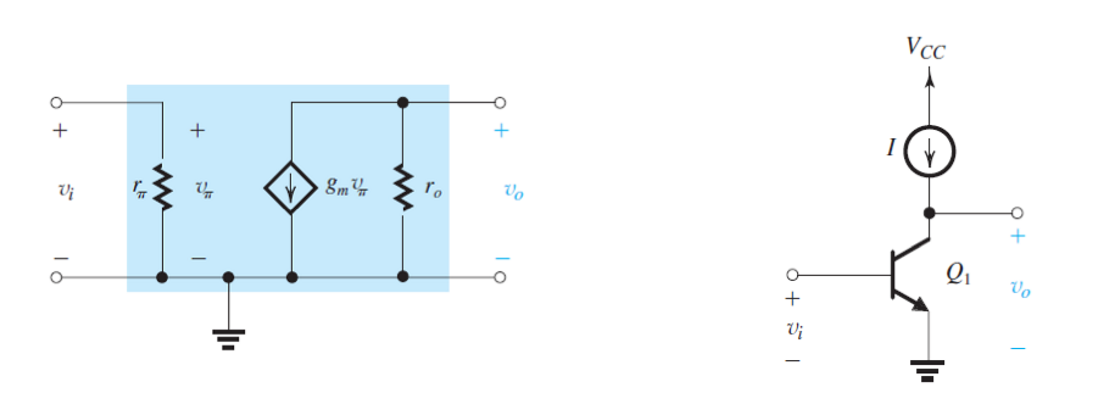
在小信号模型中对其进行分析，其开环增益应该为：
\[A_{vo}=-g_mr_o\]

电流镜在集成电路中可以为其他晶体管电路提供稳定的直流电流，在集成电路中常作为直流电流源使用。在小信号模型分析中，电流镜电路和直流电流源一样，被视为开路。

达灵顿对

达灵顿对（Darlington pair）是由两个（甚至多个）双极性晶体管组成的复合结构，通过这样的结构，经第一个双极性晶体管放大的电流可以进一步被放大。这样的结构可以提供一个比其中任意一个双极性晶体管高得多的电流增益。在使用集成电流芯片的情况里，达灵顿晶体管可以使得芯片比使用两个分立晶体管元件占用更少的空间，因为两个晶体管可以共用一个集极。

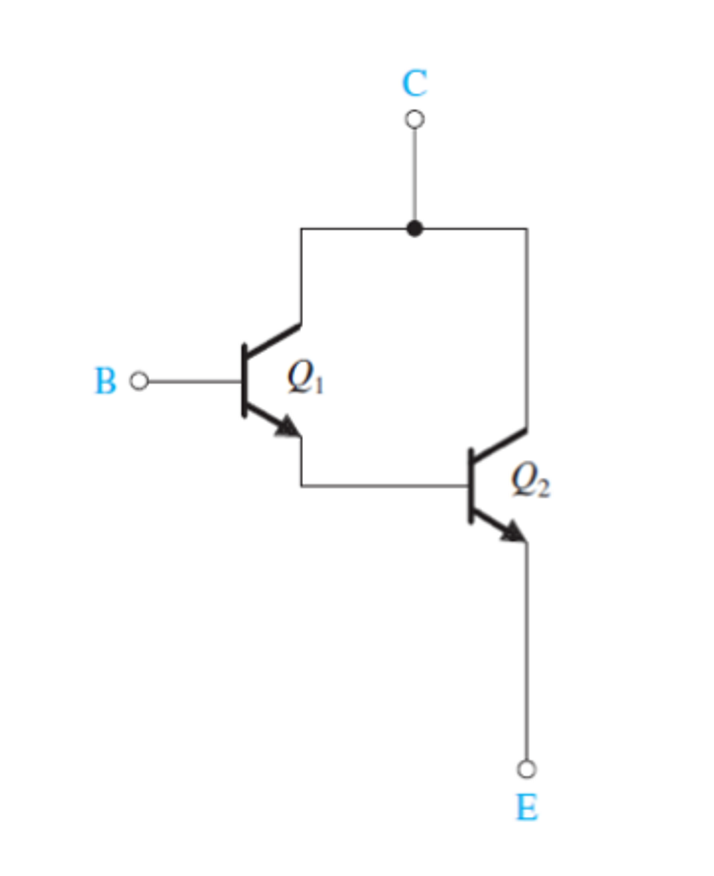
达灵顿对的电流增益可以表示为：
\[β=β_1×β_2\]

现在，达灵顿晶体管产品的典型电流增益可以达到1000甚至更高，因此只需要很小的基极电流就可以让晶体管导通。然而，这样高的电流增益也带来了一些缺点。
达灵顿对的问题在于通常\(I_{B2}\)非常小，因此\(I_{E1}\)很小，容易造成\(I_{C1}\)减小，影响\(β_1\)，使得\(Q_1\)进入截止工作状态而无法正常工作。

下图表示了\(β\)随\(I_C\)的变化曲线，可以发现如果\(I_C\)非常小的话，\(β\)无限趋近于0，晶体管进入截止状态。

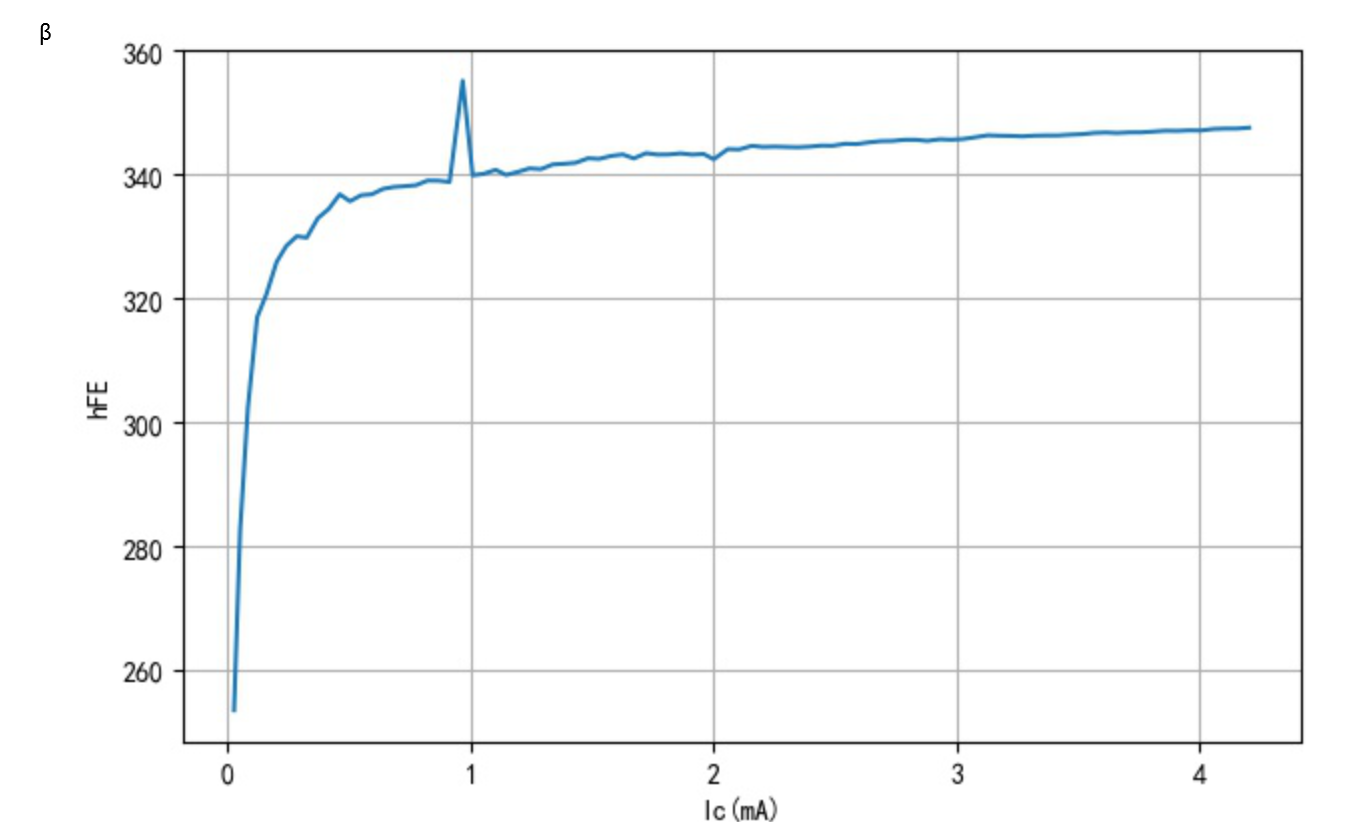
解决方法是在\(Q_1\)的发射极区增加一个恒定的电流源，使\(I_{E1}=I_{B2}+I\)，以维持\(I_{E1}\)的电流水平，使\(I_{C1}\)不至于过小。

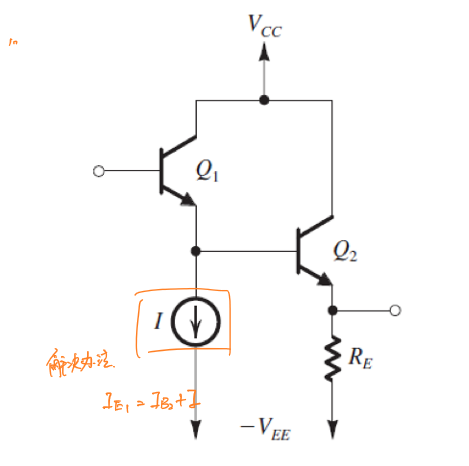
差分对

差分对是另一种常见于集成电路设计的基本结构，由于差分电路输出的结果是两个输入信号的差值，两个输入信号中携带的噪音在做差时很容易减小甚至是被除去，因此差分电路对于噪音和干扰的鲁棒性强，在集成电路中得到广泛的应用。
最基本的差分对结构如下图所示，差分对电路由两个完全相同的晶体管\(Q_1\)和\(Q_2\)组成。

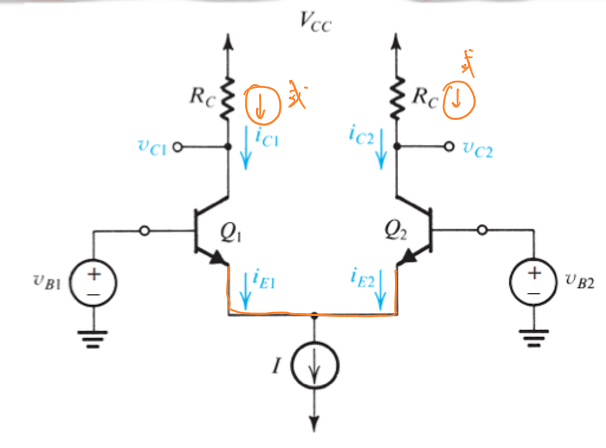
差分对电路中的两基极电压\(v_{B1}\)和\(v_{B2}\)用于设置两个晶体管状态处于放大模式或截止模式。\(i_C\)可以用电压\(V_{CC}\)加电阻\(R_C\)产生，也可以使用电流源直接产生。

差分对的正常模式

当\(v_{B1}=v_{B2}=V_{CM}\)时，晶体管处于正常模式。

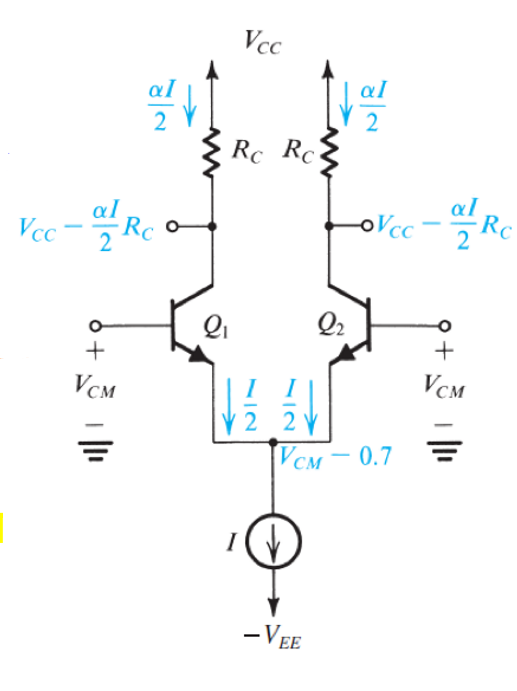
在正常模式下， \[i_{E1}=i_{E2}=\frac{I}{2}\] \[V_{C1}=V_{C2}=V_{CC}-\frac{1}{2}αIR_C\] 可以发现，\(Q_1\)和\(Q_2\)均处于放大模式，此时输出的电压\(V_{C1}\)和\(V_{C2}\)与\(V_{CM}\)没有任何关系。

差分对的差分模式

当用于设置晶体管工作状态的\(v_{B1}\)和\(v_{B2}\)不相同时，\(Q_1\)和\(Q_2\)两个晶体管中一个晶体管处于正常模式，另一个晶体管处于截止模式。 此时需要对两个晶体管的工作状态进行假设，然后观察两个晶体管的\(V_{BE}≈0.7V\)的条件是否成立，且是否与假设冲突，进而确定两个晶体管的工作状态。

在差分模式下，其中处于截止状态的晶体管的输出电压：
\[V_{C}=V_{CC}\] 处于放大状态的晶体管的输出电压：
\[V_{C}=V_{CC}-αIR_C\]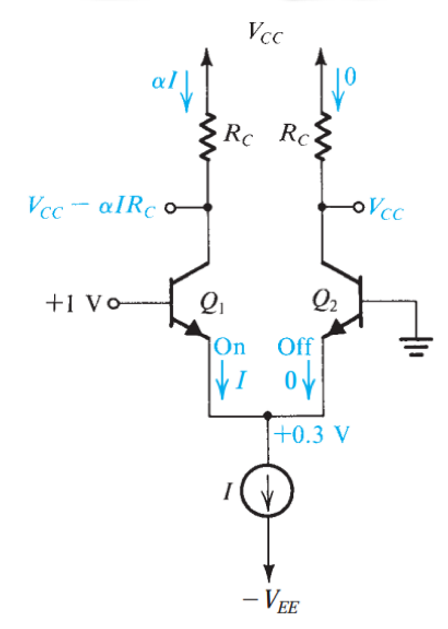

差分放大电路

差分放大电路是利用差分对性质构成的放大电路，其输入电压为两个晶体管的基极电压信号，输出两个晶体管集电极电压的差值。

大信号模型

在大信号模型下，输入的电压信号既有交流信号，也有直流信号。

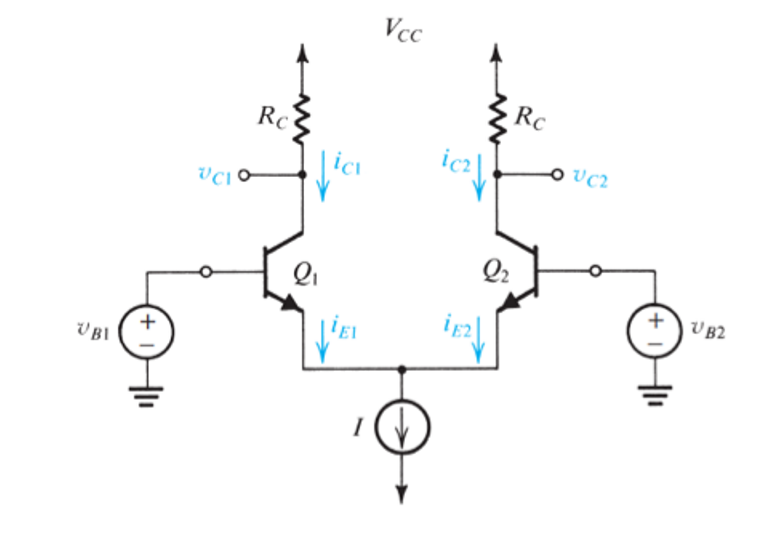
此时：
\[i_{E1}=\frac{I_S}{α}e^{(v_{B1}-v_E)/V_T}\] \[i_{E2}=\frac{I_S}{α}e^{(v_{B2}-v_E)/V_T}\] 两式子相除：
\[\frac{i_{E1}}{i_{E2}}=e^{v_{id}/V_T}\] 其中\(v_{id}\)是输入电压信号的差值：\(v_{id}=v_{B1}-v_{B2}\)。
令\(I=i_{E1}+i_{E2}\)，等式两边同时加\(1\)以带入\(I\)，得到：
\[i_{E2}=\frac{I}{1+e^{v_{id}/V_T}}≈i_{C2}\] \[i_{E1}=\frac{I}{1+e^{-v_{id}/V_T}}≈i_{C1}\] 绘制出\(i_C\)关于\(v_{id}\)的图像，即差分放大电路的大信号模型特性曲线：

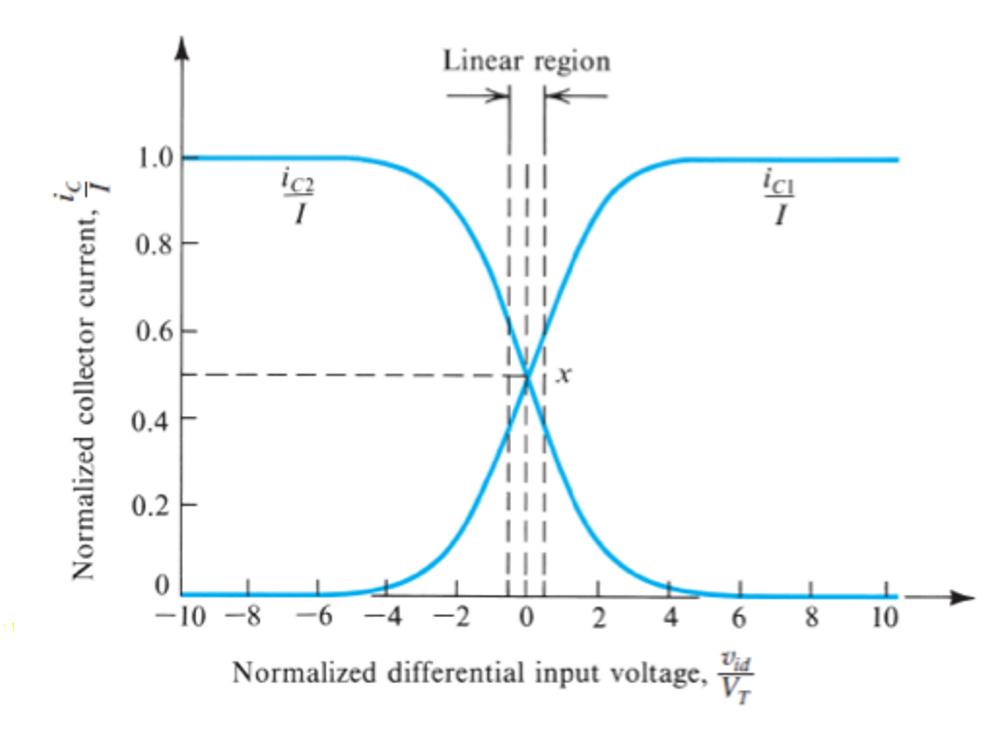
在大信号模型中找到\(v_{id}=0\)（即\(v_{B1}=v_{B2}=V_{CM}\)）附近的线性区，在这个区域中，两个晶体管可以视作是在直流工作状态的放大模式下。

小信号模型

小信号模型基于大信号模型中的线性区域进行分析，根据大信号模型中得出的结论：
\[i_{C1}=\frac{αI}{1+e^{v_{-id}/V_T}}\] \[i_{C2}=\frac{αI}{1+e^{v_{id}/V_T}}\] 对于\(i_{C1}\)，分子分母同时乘以\(e^{v_{id}/2V_T}\)：
\[i_{C1}=\frac{αIe^{v_{id}/2V_T}}{e^{v_{id}/2V_T}+e^{v_{-id}/2V_T}},V_d<<2V_T\] 利用泰勒展开式展开，并保留前两项，化简得到：
\[i_{C1}=\frac{αI}{2}+\frac{αI}{2V_T}\frac{v_{id}}{2}\] \[i_{C1}=I_C+g_m\frac{v_{id}}{2}\] 由于\(i_{C1}\)由直流分量和交流分量组成，而\(I_C\)为纯粹的直流分量，因此\(i_{C1}\)的交流分量：
\[i_{c1}=g_m\frac{v_{id}}{2}\] 同理可得：
\[i_{c2}=-g_m\frac{v_{id}}{2}\]

差分增益

通过之前的分析可以得到两个输出电压：
\[v_{C1}=V_{CC}-I_CR_C-g_mR_C\frac{v_{id}}{2}\] \[v_{C2}=V_{CC}-I_CR_C+g_mR_C\frac{v_{id}}{2}\] 定义差分电路的差分增益为输出电压信号的差值和输入电压信号的差值\(v_{id}\)之比：
\[A_d=\frac{v_{C2}-v_{C1}}{v_{id}}=g_mR_C\]

小信号模型的差分增益

对两个晶体管在小信号模型下使用T模型进行分析：

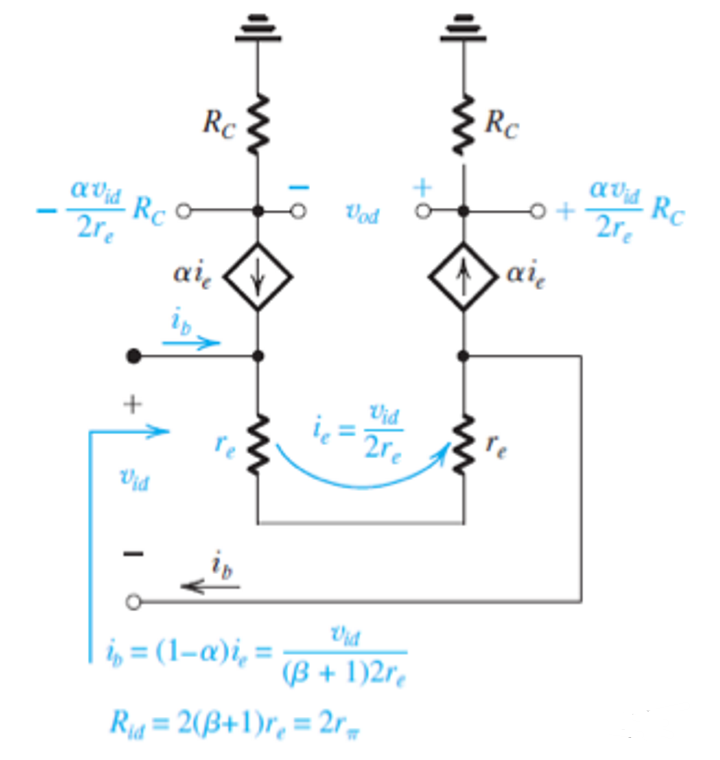
其输入电阻为：
\[R_{id}=\frac{v_{id}}{i_b}=2(β+1)r_e=2r_π\] 有:
\[i_e=\frac{v_{id}}{2r_e}≈i_c\] \[v_{c1}=-\frac{αv_{id}}{2r_e}R_C\] \[v_{c2}=\frac{αv_{id}}{2r_e}R_C\] 小信号模型下的差分增益：
\[A_d=\frac{v_{c2}-v_{c1}}{v_{id}}=\frac{2αR_C}{2r_e}≈\frac{R_C}{r_e}\]

共模抑制比

事实上，差分对的两个集电极区会有噪声和干扰，这些噪声和干扰最终归结于电路中\(R_C\)的阻值，因此在实际电路中，等效的两个\(R_C\)阻值并不完全相等，而是由细微的差异。
实际上差分对在正常模式下的两边的输出电压由于\(R_C\)细小的差异而不再相等：
\[v_{o1}=-\frac{αR_C}{r_e+2R_{EE}}v_{icm}\] \[v_{o2}=-\frac{α(R_C+ΔR_C)}{r_e+2R_{EE}}v_{icm}\] 此时整个电路相当于一个差分放大器，其在输出端存在一个差分电压：
\[v_{od}=v_{o2}-v_{o1}=-\frac{αΔR_C}{r_e+2R_{EE}}v_{icm}\] 定义共模增益为差分电压和输入电压之比：
\[A_{cm}=\frac{v_{od}}{v_{icm}}=-\frac{αΔR_C}{r_e+2R_{EE}}\]

定义共模抑制比为其差分增益与共模增益之比：
\[CMRR=\frac{A_d}{A_{cm}}\]

多极放大器

为了尽可能的减少电阻、电容带来的不稳定性，在集成电路设计中通常使用多级的电流镜、差分对组成的电路实现电流信号的多级放大。
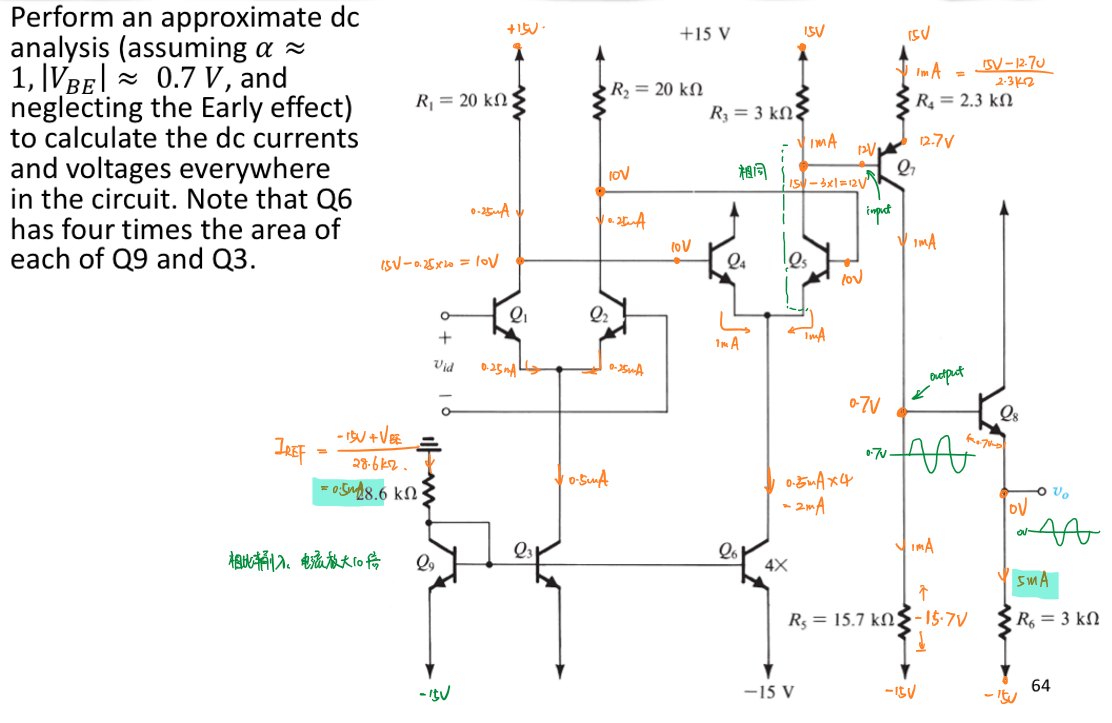
下图所示的是一个多级电流放大电路：

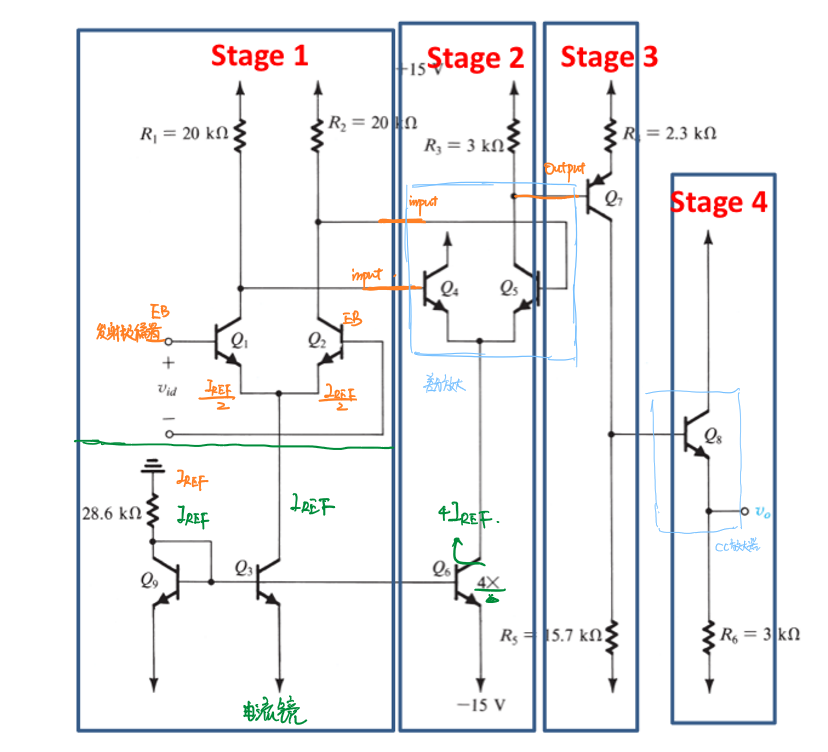
在上图的电路中，
第一级由\(Q_1\)、\(Q_2\)、\(Q_3\)、\(Q_9\) 四个晶体管组成。通过设置\(V_{EE}\),在\(Q_9\)处产生\(I_{REF}\)。\(I_{REF}\)通过\(Q_3\)、\(Q_9\) 组成的电流镜将电流信号传入\(Q_1\)、\(Q_2\)组成的差分对中，差分对将电流信号转换为电压信号，电压信号成为下一级差分对电路的输入信号。

第二级由\(Q_4\)、\(Q_5\)、\(Q_6\)三个晶体管组成。上一级输出的电压信号作为\(Q_4\)、\(Q_5\)组成的差分对电路的输入电压（控制电压），同时\(Q_6\)对第一级的电流\(I_{REF}\)进行放大，并为\(Q_4\)、\(Q_5\)组成的差分对电路提供稳定的发射极电流\(I_E\)。差分对一端输出的电压信号传入下一级，为下一级的晶体管设置工作状态。

第三级由\(Q_7\)组成，上一级差分对电路的输出电压为\(Q_7\)设置静态工作点，并通过\(R_5\)控制输入进下一级的电压信号的直流分量正好为0.7V。

第四级由\(Q_8\)组成，通过\(Q_8\)基极和发射极之间的压降将上一级电压信号的直流分量完全消除，最终输出直流分量为0的交流电压信号。同时\(R_6\)将电压信号转为电流信号，可以发现，输出端的电流信号\(I_o\)正好是\(I_{REF}\)的十倍。